

#Recureence tree hanoi towers how to
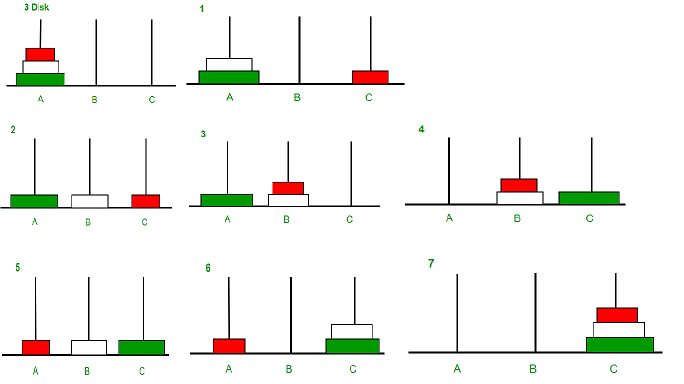
Know how to accomplish the following tasks: Therefore, for a given number N of disks, the problem appears to be solved if we After moving the bottom disk from Src to Dst these disks will have to be At this point in time all the remaining disks will have to be stacked However one solves the problem, sooner or later the bottom disk will To better understandĪnd appreciate the following solution you should try solving the puzzle for small number of disks, Let call the three pegs Src (Source), Aux (Auxiliary) and Dst (Destination).
Try IE11 or Safari and declare the site as trusted in the Java setup.

If you are reading this, your browser is not set to run Java applets. The applet expects you to move disks from the leftmost peg to the rightmost peg. You can drop a disk on to a peg when its center is sufficiently close to the center of the peg. To solve the puzzle drag disks from one peg to another following the rules. The applet has several controls that allow one to select the number of disks and observe the solution in a Fast or Slow manner. Its solution touches on two important topics discussed later on: The puzzle is well known to students of Computer Science since it appears in virtually any introductory text on data structures or algorithms. The objective is to transfer the entire tower to one of the other pegs (the rightmost one in the applet below), moving only one disk at a time and never a larger one onto a smaller. We are given a tower of eight disks (initially four in the applet below), initially stacked in increasing size on one of three pegs. The Tower of Hanoi puzzle was invented by the French mathematician Edouard Lucas in 1883.


 0 kommentar(er)
0 kommentar(er)
